経済学で出る数学

ワークブックでじっくり攻める：問1.17

1. 座席が $50$ 席売れた場合
• $収入=5,000 \times 50 = 250,000$ 円
• $総費用=150,000$ 円
• $利潤=250,000-150,000=100,000$円


2. 座席が $x$ 席売れた場合
• $収入=5,000 \times x = 5,000 x$ 円
• $総費用=150,000$ 円
• $利潤=5,000 x-150,000$ 円


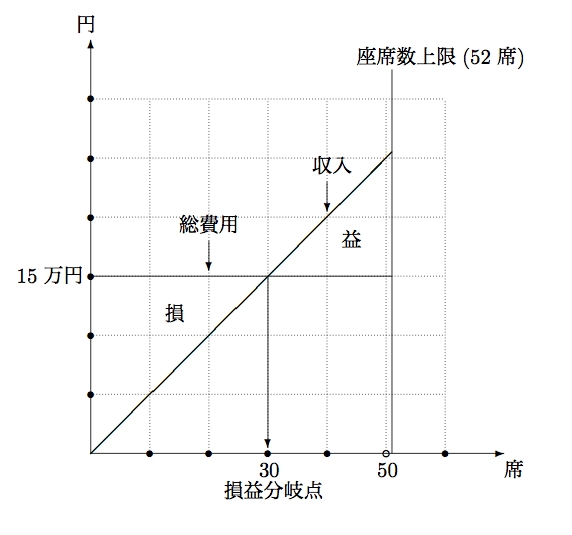
3. 損益分岐点
• $利潤=5,000 x-150,000=0$，すなわち，$5,000 x=150,000$ を解いて，$x=30$ 席


4. 損益分岐点比率
• $\dfrac{30}{52}\approx 0.58$，すなわち，$58\%$


5. $\dfrac{平均費用}{価格}$
• $2,900 \div 5,000 = 0.58$となり，損益分岐点比率に一致する．

• $平均費用=\dfrac{総費用}{総座席数}=\dfrac{150,000}{52}\approx 2900$
• 損益分岐点では，$総費用=収入$ で $収入=価格 \times 損益分岐点数$ なので $価格=\dfrac{総費用}{損益分岐点数}$