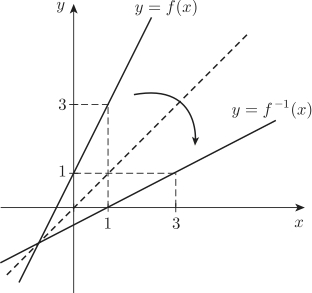
次の変形を行えばよい. \begin{eqnarray} y=2x+1&\Longleftrightarrow & 2x=y-1\\[2ex] &\Longleftrightarrow & x=\dfrac{1}{2}y-\dfrac{1}{2}\\ \end{eqnarray} したがって,$f^{-1}(y)=\dfrac{1}{2}y-\dfrac{1}{2}$ であるが,説明変数を $x$ ,被説明変数を $y$ とするのが通例なので,$x$ と $y$ を入れ替えた $f^{-1}(x)=\dfrac{1}{2}x-\dfrac{1}{2}$ が逆関数である.$y=f(x)$ と $y=f^{-1}(x)$ を同一の図に描くと,45度線での折り返しになる.

◎問題変更 $f(x)=2x+1$ → $f(x)=2x+2$ を踏まえると:
\begin{eqnarray}
y=2x+2&\Longleftrightarrow & 2x=y-2\\[2ex]
&\Longleftrightarrow & x=\dfrac{1}{2}y-1\\
\end{eqnarray}
したがって,$f^{-1}(x)=\dfrac{1}{2}x-1$ である
同様に次の変形を行えばよい. \begin{eqnarray} q=40-2p&\Longleftrightarrow & 2p=40-q\\[2ex] &\Longleftrightarrow & p=20-\dfrac{1}{2}q\\ \end{eqnarray} したがって,$D^{-1}(q)=20-\dfrac{1}{2}q$ であるが,こんどは説明変数と被説明変数の入れ替えはおこなわない. マーシャルの記法に従って$p$(価格)を縦軸にしてグラフを描くからである.$P(q)=D^{-1}(q)$ は需要関数の逆関数であることから,逆需要関数とよばれる.