経済学で出る数学

ワークブックでじっくり攻める：問1.9

1. 1. 逆需要関数は $D(p)$ の逆関数．したがって \begin{eqnarray} q&=&30-\dfrac{3}{4}p \tag{需要関数}\\[2ex] p&=&40-\dfrac{4}{3}q \tag{逆需要関数} \end{eqnarray}
   
   
   2. 逆需要関数は $D(p)$ の逆関数．したがって \begin{eqnarray} p&=&40 \tag{$p$切片}\\[2ex] q&=&30 \tag{$q$切片} \end{eqnarray}
   
   
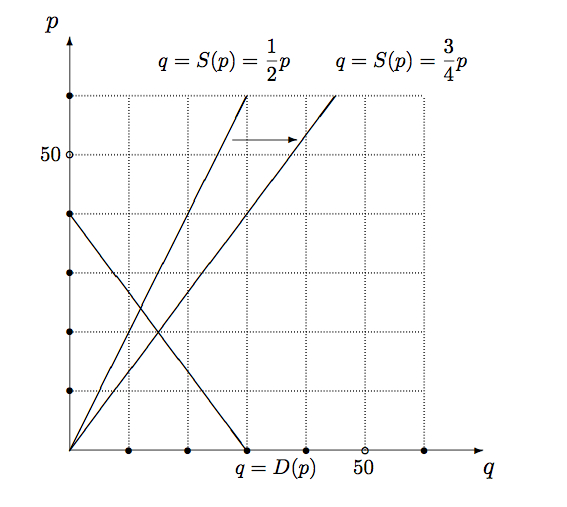
   3. $S(40)=\dfrac{1}{2}\times 40=20$．これで供給曲線は原点と$(20,40)$ を結べばよいことがわかる $(p, q)$ の順であることに注意しないと，マーシャルの罠に落ちる．
   
   
   4. 市場均衡は，次の連立方程式を解けば， \begin{eqnarray} q&=&30-\dfrac{3}{4}p\\[2ex] q&=&\dfrac{1}{2}p \end{eqnarray} $30-\dfrac{3}{4}p=\dfrac{1}{2}p \Longleftrightarrow 30=\dfrac{5}{4}p$ なので$p=24$，$q=12$ となる．
   
   
2. 新しい市場均衡は，次の方程式を解けばよい． \begin{eqnarray} q&=&30-\dfrac{3}{4}p\\[2ex] q&=&\dfrac{3}{4}p \end{eqnarray} $30-\dfrac{3}{4}p=\dfrac{3}{4}p \Longleftrightarrow 30=\dfrac{6}{4}p$ なので$p=20$，$q=15$ となる．供給量が増えることで，均衡価格は下った．