本問は『経出る』6.3.2(pp.187)の別解説でもある.
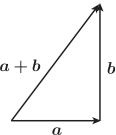
(1)三平方の定理から \[ a \perp b \Longleftrightarrow |a|^2+|b|^2=|a+b|^2 \tag{1} \] が成り立つことを思い出すと, \begin{eqnarray} (1)の左辺&=&(a_1^2+a_2^2)+(b_1^2+b_2^2)\\ (1)の右辺&=&(a_1+a_2)^2+(b_1+b_2)^2\\ &=&(a_1^2+a_2^2)+(b_1^2+b_2^2)+2(a_1b_1+a_2b_2) \end{eqnarray} なので,$a \perp b \Longleftrightarrow a_1b_1+a_2b_2=a\cdot b=0$

(2) $a \perp b \Longleftrightarrow a\cdot b \Longleftrightarrow a_1b_1+a_2b_2=0 \Longleftrightarrow a_1(-b_1)+a_2(-b_2)=0 \Longleftrightarrow a\cdot (-b)=0 \Longleftrightarrow a \perp -b$ .