経済学で出る数学

ワークブックでじっくり攻める：問7.21解答例

1. ラグランジュ乗数法の解を示す．
• 【Step1】ラグランジュ関数を作ると， $ {\cal{L}}(x,y,\lambda)=xy+\lambda\left(4-x-y\right). $


• 【Step2】 各変数で偏微分してイコールゼロとおくと， \[ \left\{ \begin{array}{lll} 0=\displaystyle \frac{\partial\cal{L}}{\partial x} =y-4{\lambda} & \rightarrow y={4{\lambda}} &\qquad (1)\\[2ex] 0=\displaystyle \frac{\partial\cal{L}}{y} =x-4{\lambda}y & \rightarrow x={4{\lambda}} &\qquad (2)\\[2ex] 0=4-x-y& & \qquad (3) \end{array} \right. \]


• 【Step3】 あとは工夫して解く．
  • $(1), (2)$ を $(3)$ に代入すると， $4-{4{\lambda}}-{4{\lambda}}=0$, ゆえに $\lambda =\dfrac{1}{2}$．
  
  
  • $(1)$ から，$y=2$
  
  
  • $(2)$ から，$x=2$
  
  
  ゆえに最適解は，$(x,y)=\left(2, 2\right)$ であり，連立方程式 \[ \left\{ \begin{align} x+4&=4\\ y&=\dfrac{3}{x} \end{align} \right. \] の解，$(1,3), (3,1)$ のいずれとも異なる．


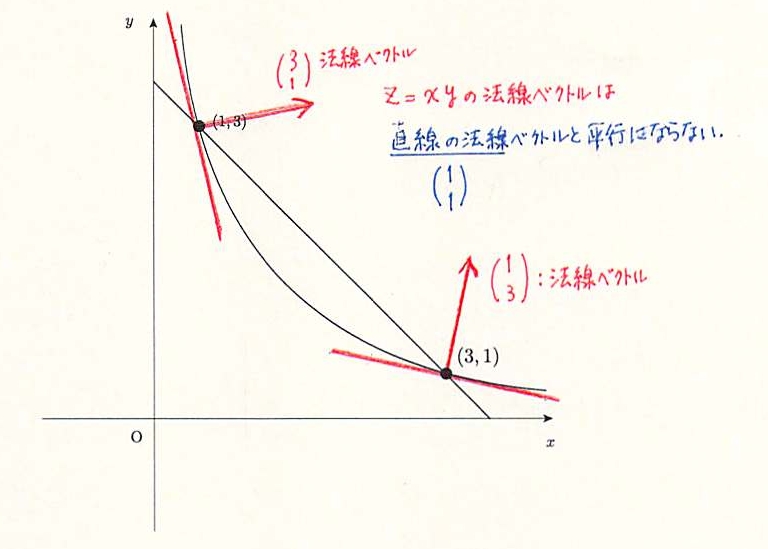
• 図説は下図の通り．最適解になるためには， $y=\dfrac{3}{x} \Leftrightarrow xy=3$ と見れば，効用関数 $z=xy$ の値が，まだ大きくなって，右上方に移動しないといけない．