経済学で出る数学

ワークブックでじっくり攻める：問7.22解答例

1. 連立方程式， \[ \left\{ \begin{align} x+2y&=10　\cdots (1)\\[1ex] x^2+y^2&=20　\cdots (2) \end{align} \right. \] を解く．$(1)$ より，$x=10-2y$．これを $(2)$ に代入して， $(10-2y)^2+y^2=20 \Leftrightarrow 5y^2 - 40y +80=0 \Leftrightarrow y^2-8y+16=0 \Leftrightarrow (y-4)^2=0$ から，$y=4, x=2$．


2. $１．$の解がラグランジュ乗数法の解であることを示す．
• 【Step1】ラグランジュ関数を作ると， $ {\cal{L}}(x,y,\lambda)=x^2+y^2+\lambda\left(10-x-2y\right). $


• 【Step2】 各変数で偏微分してイコールゼロとおくと， \[ \left\{ \begin{array}{lll} 0=\displaystyle \frac{\partial\cal{L}}{\partial x} =2x-{\lambda} & \rightarrow x=\dfrac{{\lambda}}{2} &\qquad (3)\\[2ex] 0=\displaystyle \frac{\partial\cal{L}}{y} =2y-2{\lambda} & \rightarrow y={\lambda} &\qquad (4)\\[2ex] 0=10-x-2y& & \qquad (5) \end{array} \right. \]


• 【Step3】 あとは工夫して解く．
  • $(3), (4)$ を $(5)$ に代入すると， $10-\dfrac{\lambda}{2}-2{\lambda}=0$, ゆえに $\lambda =4$．
  
  
  • $(3)$ から，$x=2$
  
  
  • $(4)$ から，$y=4$
  
  
  ゆえに最適解は，$(x,y)=\left(2, 4\right)$ であるが，これは連立方程式 \[ \left\{ \begin{align} x+2y&=10\\[1ex] x^2+y^2&=20 \end{align} \right. \] の解でもある．


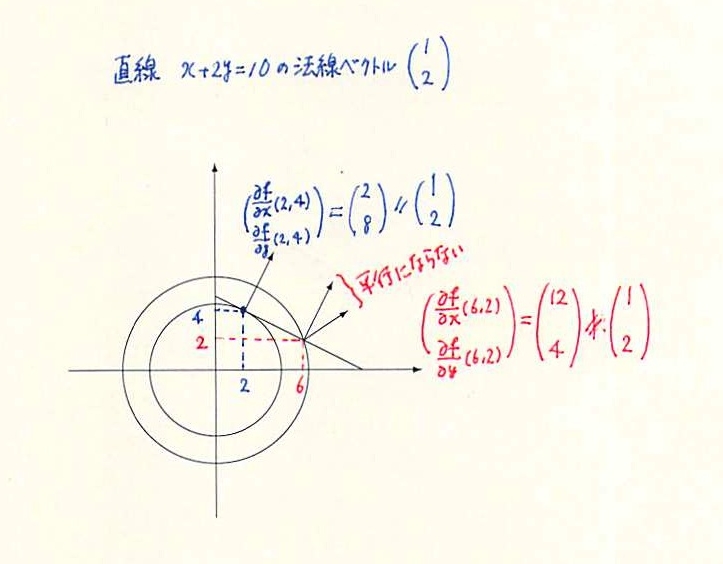
• 図説は下図の通り．最適解で接している．実際， $\begin{pmatrix} \displaystyle \frac{\partial f}{\partial x}(2,4)\\ \displaystyle \frac{\partial f}{\partial y}(2,4) \end{pmatrix} = \begin{pmatrix} 2\\ 8 \end{pmatrix} $ ， $\begin{pmatrix} \displaystyle \frac{\partial g}{\partial x}(2,4)\\ \displaystyle \frac{\partial g}{\partial y}(2,4) \end{pmatrix} = \begin{pmatrix} 1\\ 2 \end{pmatrix} $ 　 ∴　 $ \begin{pmatrix} 2\\ 8 \end{pmatrix} =4 \begin{pmatrix} 1\\ 2 \end{pmatrix} $ ．





3. $(6,2)$ がラグランジュ乗数法の解ではないことを示す． $\begin{pmatrix} \displaystyle \frac{\partial f}{\partial x}(6,2)\\ \displaystyle \frac{\partial f}{\partial y}(6,2) \end{pmatrix} = \begin{pmatrix} 12\\ 4 \end{pmatrix} $ ， $\begin{pmatrix} \displaystyle \frac{\partial g}{\partial x}(6,2)\\ \displaystyle \frac{\partial g}{\partial y}(6,2) \end{pmatrix} = \begin{pmatrix} 1\\ 2 \end{pmatrix} $ 　 ∴　 $ \begin{pmatrix} 12\\ 4 \end{pmatrix} \neq \lambda \begin{pmatrix} 1\\ 2 \end{pmatrix} $ ．

本紙では小問3.でラグランジュ乗数法の解でないことを調べる，解候補として $(x,y)=(3,2)$ を指示したが，そもそもこれは制約式 $x+2y=10$ を満たさないので，論外．制約式を満たす解のことを，実行可能解というが，本問では，そもそも実行可能解ではないものを指示してしまった，うっかりミス．