経済学で出る数学

ワークブックでじっくり攻める：問7.4(1)解答例

• 【Step 1】偏微分する． \begin{align} \dfrac{\partial f}{\partial x}(x,y)&=\dfrac{1}{2}x^{-\frac{1}{2}}y^{\frac{2}{3}}-1 \\ \dfrac{\partial f}{\partial y}(x,y)&=\dfrac{2}{3}x^{\frac{1}{2}}y^{-\frac{1}{3}}-2 \end{align}


• 【Step 2】$1$階条件から導かれる方程式は， \[ \left\{\begin{align} \dfrac{1}{2}x^{-\frac{1}{2}}y^{\frac{2}{3}}&=1　\cdots　(1)\\ \dfrac{2}{3}x^{\frac{1}{2}}y^{-\frac{1}{3}}&=2　\cdots　(2) \end{align} \right. \] $(1)\div (2)$ を作ると $3x^{-1}y=2$．ゆえに $y=\dfrac{2}{3}x$．(1) に代入すると $\dfrac{1}{2}x^{-\frac{1}{2}}\left(\dfrac{2}{3}\right)^{\frac{2}{3}}x^{\frac{2}{3}} =\dfrac{1}{2}x^{\frac{1}{6}}\left(\dfrac{2}{3}\right)^{\frac{2}{3}}=1\Longleftrightarrow x^{\frac{1}{6}}=2\times \left(\dfrac{3}{2}\right)^{\frac{2}{3}}$． ゆえに，$x=2^6\times \left(\dfrac{3}{2}\right)^{\frac{2}{3}\times 6}=2^2\times 3^4$．$y=\dfrac{2}{3}\times 2^2\times 3^4=2^3\times 3^3$． 以上より， $(x,y)=(2^2\times 3^4,2^3\times 3^3)$ が$1$階条件を満たす．

1. $(x,y)=(2^23^4,2^33^3)$ は最大解でも最小解でもない．それは次の数値例から確認できる．
• $f(2^23^4, 2^33^3)$$= (2^23^4)^{\frac{1}{2}}(2^33^3)^{\frac{2}{3}}-2^23^4-2\cdot 2^33^3 =2^33^4-2^23^4-2^43^3=2^23^3(2\times 3-3^2-2^2)=2^23^3(6-3-4)= -(2^23^3)$
• $f(2^23^4, 2^63^3)= (2^23^4)^{\frac{1}{2}}(2^63^3)^{\frac{2}{3}}-2^23^4-2\cdot 2^63^3 =2^53^4-2^23^4-2^73^3=2^23^3(2^33-3-2^53) =2^23^3(24-3-96)=-75(2^23^3)$
• $f(0, 0)=0$
まとめると，$f(2^23^2, 2^63^3)$ < $f(2^23^4, 2^33^3)$$ < $f(0, 0)．


2. 気づいたのは second derivative test（『経出るの範囲外） を行ったのがきっかけ．
   \[ \left| \begin{array}{cc} \dfrac{{\partial}^2 f}{\partial x^2}(x,y) & \dfrac{{\partial}^2 f}{\partial y \partial x}(x,y)\\ \dfrac{{\partial}^2 f}{\partial x \partial y}(x,y) & \dfrac{{\partial}^2 f}{\partial y^2}(x,y) \\ \end{array} \right| = \left| \begin{array}{cc} \dfrac{-1}{4}x^{-\frac{3}{2}}y^{\frac{3}{2}} & \dfrac{1}{3}x^{-\frac{1}{2}}y^{-\frac{1}{2}} \\ \dfrac{1}{3}x^{-\frac{1}{2}}y^{-\frac{1}{2}} & \dfrac{-2}{9}x^{\frac{1}{2}}y^{-\frac{3}{4}} \\ \end{array} \right| =\dfrac{1}{18}x^{-1}y^{-\frac{2}{3}}-\dfrac{1}{9}x^{-1}y^{-\frac{2}{3}} < 0 \] となり，second derivative test　失格である．


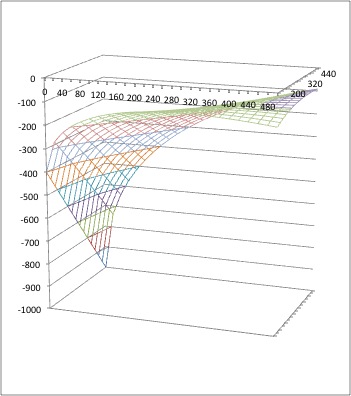
3. やや見づらいが$(2^23^4, 2^33^3)=(324,216)$が鞍点になっているのが分かる．
   
   


4. 本問は本来，問7.5にもってくればよかった．