経済学で出る数学

ワークブックでじっくり攻める：問7.5(2)解答例

• 【Step 1】偏微分する．$f(x,y)=(y-x^2)(y-2x^2)=y^2-2x^2y-x^2y+2x^4=y^2-3x^2y+2x^4$ と展開しておく． \begin{align} \dfrac{\partial f}{\partial x}(x,y)&=-6xy+8x^3=-6xy+8x^3 \\ \dfrac{\partial f}{\partial y}(x,y)&=2y-3x^2 \end{align}


• 【Step 2】$1$階条件から導かれる方程式は， \[ \left\{\begin{align} -6xy+8x^3&=0　\cdots　(1)\\ 2y-3x^2&=0　\cdots　(2) \end{align} \right. \] $(2)$ より $y=\dfrac{3}{2}x^2$．したがって．$(1)$ より $-6x \times \dfrac{3}{2}x^2+8x^3=-9x^3+8x^3=-x^3=0$．ゆえに$x=0, y=0$ 以上より，$1$階条件を満たす解は $(x,y)=(0,0)$ である．

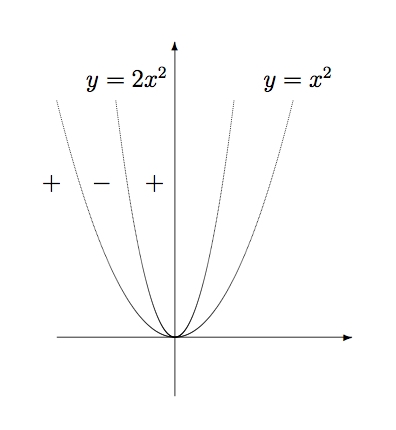
下図からもわかるように，$1$階条件を満たす解 $(x,y)=(0,0)$ は極大でも極小でもない．