経済学で出る数学
ワークブックでじっくり攻める:応用問題
面積比較による不等式評価
【問】 面積を比較することで,次の不等式を示しなさい.$n$は自然数とする.
\[
\dfrac{1}{n+1}< \log_{}{\Bigl(1+\dfrac{1}{n}\Bigr)}<\dfrac{1}{n}.
\]
【解答】
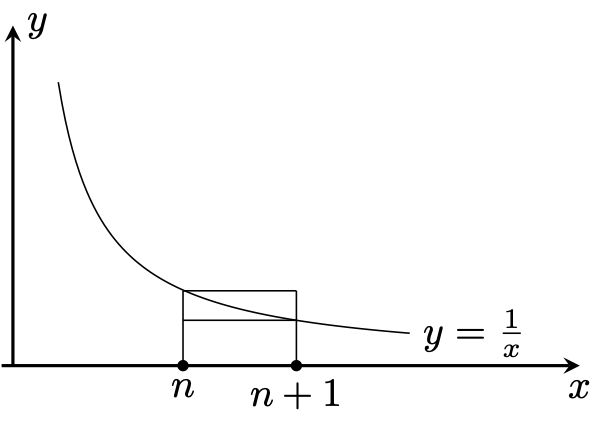
下図より,
\[
\dfrac{1}{n+1}< \int_{n}^{n+1}\dfrac{1}{x}dx <\dfrac{1}{n},
\]
だが,
\[
\int_{n}^{n+1}\dfrac{1}{x}dx =\Bigl[\log_{}{x}\Bigr]_{n}^{n+1}=\log_{}{n+1}-\log_{}{n}
=\log_{}{\dfrac{n+1}{n}}=log_{}{\Bigl(1+\dfrac{1}{n}\Bigr)}.
\]
【解答終】
【Further Reading】
S.Lang, A First Course in Calculus Fifth Edition. Springer(1986)
ふろく(2)応用問題 一覧へ