経済学で出る数学

ワークブックでじっくり攻める：応用問題

【問】　コーヒー豆の需要関数が \[ D(p)=100-p \] であるとしよう．また供給関数が \[ S(p)=3p \] であるとする．コーヒー豆の市場は需要者（消費者）たるS社の買手独占であるとする．
S社は買値をいくらにしたときに，余剰が最大になるか求めなさい．

【解答】

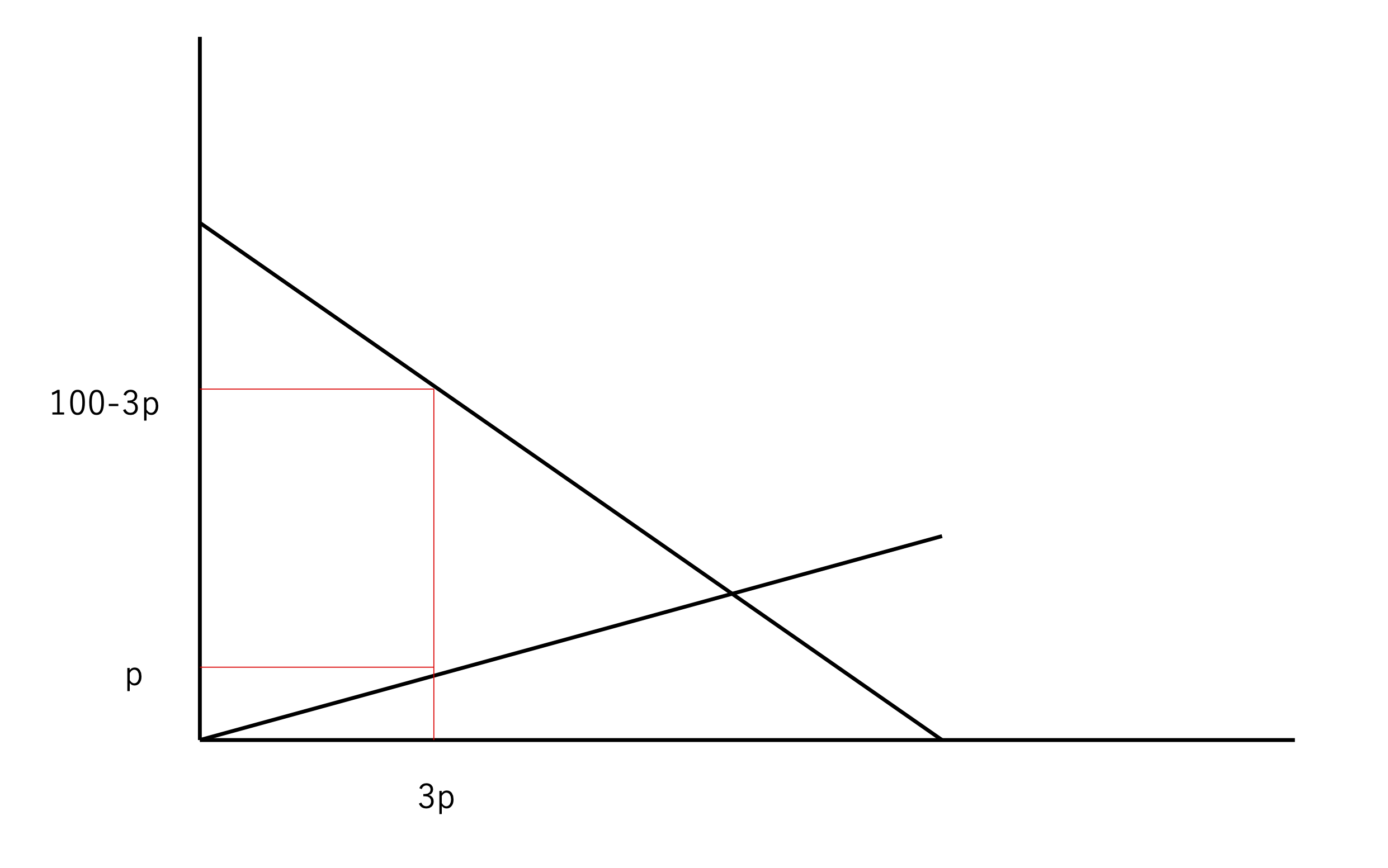
買値を$p$円露する．消費者余剰$CS$は \[ CS=\dfrac{3p(100-p)+(100-4p)}{2}=\frac{3p(200-5p)}{2} \] なので，$p=\dfrac{40+0}{2}=20$のときに最大となる．

【解答終】

【Further Reading】田中久稔『大学の人気講義でよく分かる「ミクロ経済学」超入門』SBクリエイティブ（2022））