経済学で出る数学
ワークブックでじっくり攻める:応用問題
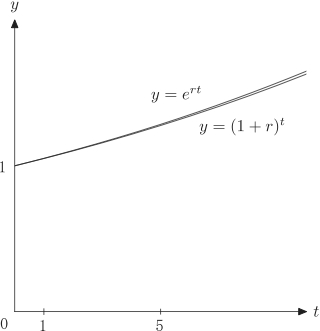
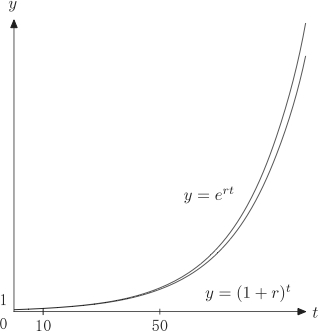
不等式 $e^{rt}\geq (1+r)^t$(『経出る』図3.6)
不等式
\[
e^{rt}\geq (1+r)^t
\]
が成り立つことを示しなさい.
【解答1】
\[
e^{rt}=\Bigl(\lim_{k\to \infty}\Bigl(1+\dfrac{r}{k}\Bigr)^{k}\Bigr)^t
=\lim_{k\to \infty}\Bigl(1+\dfrac{r}{k}\Bigr)^{kt}
\]
なので,
$\Bigl(1+\dfrac{r}{k}\Bigr)^{k}$が,$k$について単調増加であることを示せば,
$\Bigl(1+\dfrac{r}{k}\Bigr)^{k}\geq \Bigl(1+\dfrac{r}{1}\Bigr)^{1}=(1+r)$
より,
\[
\Bigl(1+\dfrac{r}{k}\Bigr)^{kt}\geq (1+r)^t
\]
を得るので,
$k\to \infty$とすればよい.単調増加であることを示すためには,一般化された相加相乗平均の不等式
\[
\dfrac{a_1+a_2+\cdots +a_{k+1}}{k+1}
\geq \sqrt[k+1]{a_1a_2\cdots a_{k+1}}
\]
を使う.$a_1=a_2=\cdots =a_k=\dfrac{k+r}{k}, a_{k+1}=1$として,不等式を使うと,
\begin{align}
\dfrac{\dfrac{k+r}{k}k+1}{k+1}&\geq
\sqrt[k+1]{\Bigl(\dfrac{k+r}{k}\Bigr)^k}\\
\Bigl(\dfrac{k+1+r}{k+1}\Bigr)^{k+1}
&\geq \Bigl(\dfrac{k+r}{k}\Bigr)^k\\
\Bigl(1+\dfrac{r}{k+1}\Bigr)^{k+1}
&\geq \Bigl(1+\dfrac{r}{k}\Bigr)^k
\end{align}
を得る.
【解答1終】
【解答2】
$f(t)=\dfrac{e^{rt}}{(1+r)^t}$とおいたとき,$f(t)\geq 1$であることを示せばよい.準備として$r>0$に対し,$g(r)=r-\log_{}{1+r} > 0$であることを示す.
\[
g^{\prime}(r)=1-\dfrac{1}{1+r}=\dfrac{r}{1+r} > 0
\]
より,$g(r)$は単調増加.従って$r>0$に対し,$g(r) > g(0)=0$.一方,
\begin{align}
f^{\prime}(t)&=\dfrac{re^{rt}(1+r)^t
-e^{rt}(1+r)^t\log_{}{1+r}}{(1+r)^{2t}}\\
&=\dfrac{e^{rt}}{(1+r)^{t}}\bigl(r-\log_{}{1+r}\bigr) > 0
\end{align}
なので,$f(t)$は単調増加.従って$t>0$に対し,$f(t) > f(0)=1$を得る.
【解答2終】
【メモ】
『経出る』図3.6は以下の通り.$r=0.05$で描かれている.
【メモ終】
ふろく(2)応用問題 一覧へ