経済学で出る数学
ワークブックでじっくり攻める:応用問題
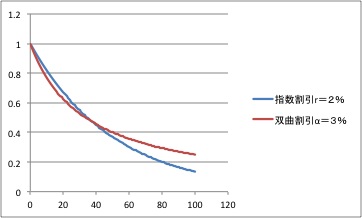
双曲割引(単利による割引)と指数割引(複利による割引)の逆転現象:連続時間(2015.11.26作成)
$c$円を単利,利子率$R$で割引くと$\dfrac{c}{(1+Rt)}$円,
複利,利子率$r$で割引くと
$ce^{-rt}$円であるが,両者の逆転現象を示す.
$\dfrac{1}{(1+Rt)}$ と $e^{-rt}$ の大小を考察しなさい.
【解答】
$R>r$とする
\[
f(t)=(1+Rt)-e^{rt}
\]
とおく.微分すると $f^{\prime}(t)=R-re^{rt}$ なので,$1$階条件を求めると,
$t=\dfrac{1}{r}\log_{}{\dfrac{R}{r}}$.
$2$階微分は,$f^{\prime\prime}(t)=-r^2e^{rt}< 0 $ なので,ここで最大値をとる.最大値を計算すると,$R\approx r$ に対し
\begin{align}
f\Bigl(\dfrac{1}{r}\log_{}{\dfrac{R}{r}}\Bigr)&
=\Bigl(1+\dfrac{R}{r}\log_{}{\dfrac{R}{r}}\Bigr)-e^{\log_{}{\dfrac{R}{r}}}\\
&=\Bigl(1+\dfrac{R}{r}\log_{}{\dfrac{R}{r}}-{\dfrac{R}{r}}\Bigr)\\
&>1-{\dfrac{R}{r}}>0.
\end{align}
【註】
$\dfrac{1}{r}\log_{}{\dfrac{R}{r}} < t $では減少関数で,
$\lim_{t\to \infty}(1+Rt)-e^{rt}= -\infty$ なのでいずれ,$f(t)<0$となる.
まとめると$f>0$ の領域:$f(0)=0 \nearrow \max_{t}f(t)>0 \searrow f< 0$ の領域.
\begin{align}
f>0 の領域:& \dfrac{1}{(1+Rt)} < e^{-rt} \\
f<0 の領域:& \dfrac{1}{(1+Rt)} > e^{-rt} .
\end{align}
となり,逆転現象が起きる.
【解答終】
【Further Reading】
池田新介『自滅する選択』東洋経済(2012)第3章
ふろく(2)応用問題 一覧へ