経済学で出る数学
ワークブックでじっくり攻める:応用問題
準凸関数の最小点と極小点
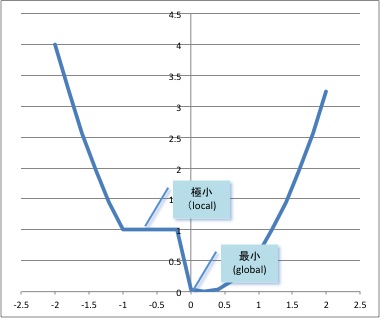
準凸関数の最小値の大域性は,凸関数よりやや制限が加わる.凸関数のときは,
$極小 \Rightarrow 最小$ だったが,準凸関数の場合は下図に見るようにかならずしもそうは言えない.
【問】いま $f$ が準凸関数であるとき,狭義の極小点は狭義の最小点であることを示しなさい.
【解答】
$x^*$ を $f$ の狭義の極小点とする.すなわち,どんな $y\neq x^*$ に対しても,
$y$ が $x^*$ に十分近ければ、$f(x^*) < f(y)$ となっている.
$x^*$ が狭義の最小点であることを否定してみよう.
すると $f(\bar{x})\leq f(x^*)$ となる $\bar{x}\neq x^*$ があることになる.
$f(x)$ が準凸関数であることより,
$0 \leq \lambda \leq 1$ を満たすどんな
$\lambda$ に対しても,
\[
f((1-\lambda )x^*+\lambda \bar{x}) \leq f(x^*)
\]
となる.したがって,
$\lambda \to 0$ とすると,$x^*$ の狭義の極小性に反することになる.
【解答終】
【Further Reading】
M. Avriel, ‘Nonlinear Programming: Analysis and Methods’, Prentice Hall(1976)
ふろく(2)応用問題 一覧へ