

T市での去年のゴールデン・ウィークの「おだんご」の需要,供給は以下の$1$次関数であった. ただし $p$ がおだんごの価格,$q$ が売上量である.このときマーシャルの罠に落ちないように気をつけながら, 需要曲線 $q=D(p)$ および,供給曲線 $q=S(p)$ を $qp$ 平面上に図示しなさい.また,市場均衡を求めなさい.
\[ \begin{array}{c@{ \;}c@{ \;}ll} D(p)&=& \displaystyle 40-2p& \cdots \quad 需要 \quad (1) \\[2mm] S(p)&=& \displaystyle 2p & \cdots \quad 供給 \quad (2) \end{array} \]

製薬会社とT大は共同開発したサプリメント『$\heartsuit$T大チューリップちゃん』を大学発ブランドとして売り出した.需要関数は \[ q=D(p)=500-\frac{1}{2}p \] で与えられている.また費用は$1$箱あたり$400$円であるとする. 利潤を最大にするためには,何円で売ればよいか,横軸切片を使って調べなさい.


|
|
|---|


(1)徹夜で仕事をした久美さんは,国立駅で降りるところを八王子まで行き,折り返しても三鷹まで行き,立川まで行き,$4$度目でやっと国立で下車した.$t$ 回目に寝過ごした駅数を $a_t$ とする.また,$t$ 回目に寝過ごした時間(分)を $b_t$ とする. $a_t$ と $b_t$ はどのような値になるだろうか?ただし,沿線のJRの駅と各駅間の所要時間は以下の通りである.


|

|
|---|

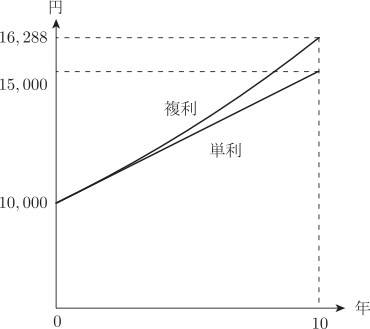
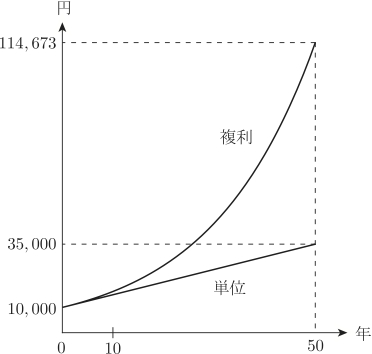
(2)利子率を$r=0.05$とする.毎年,$100$万円を積み立てて預け入れる.$10$年目に預け入れた直後の時点での口座残高を求めなさい.


(1)次の関数を微分しなさい.


(2)Y$\heartsuit$RIK$\heartsuit$は,夏休みにバイトで$18$万円をかせいだ(よくやった). このうち今年は $x$ 円を使い,$s$ 円を貯金する.来年は利息でふくらませた残高 $y$ 円を使おうと考えている. Y$\heartsuit$RIK$\heartsuit$の満足度 $u$ は積 $u = x y$ でわかるものとする.Y$\heartsuit$RIK$\heartsuit$は今年何円使うのだろうか. 以下の指示に従い,求めなさい. ただし貯金には年$5\%$の利子がつくものとする.


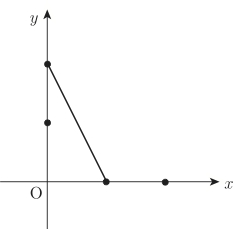
(1)ポー市のスーパーでは牛肉$1$ kgを $10$ ユーロ,ワイン$1$ リットルを $5$ ユーロで売っている. ジョン・ポールは $100$ ユーロ持って買い物に出かけた.

|
|
|---|

(2)$A$を凸集合とし,$x_i$が$A$に含まれるとする.また$0 \leq {\alpha}_i \leq 1$,$i=1,2,\ldots , N$で ${\alpha}_1+{\alpha}_2+\cdots +{\alpha}_N=1$とする.このとき, \[ {\alpha}_1\mbox{$x_1$}+{\alpha}_2\mbox{$x_2$}+\cdots + %{\alpha}_n\mbox{$x_N$} {\alpha}_N\mbox{$x_N$} \] が$A$に含まれることを示せ.
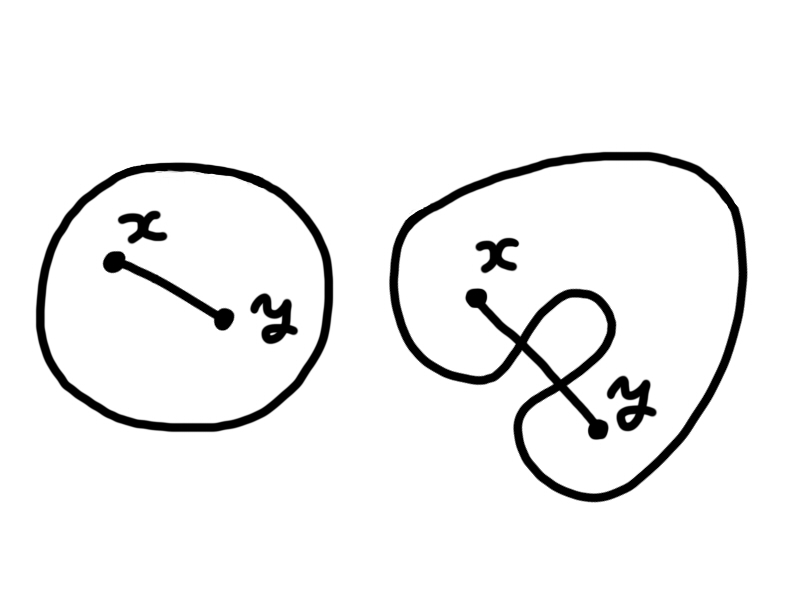

ラグランジュの未定乗数法を使って次の最小化問題を解きなさい. \[ \begin{array}{cl} \displaystyle \min_{x,y}& f(x,y)=x^2+3y^2 \\[2ex] s.t.& 2x+3y=7 \end{array} \]
